Nothing special here. It’s just a blog post for summarising my algorithm learning course. Although this was already taught in the University, I remember nothing about it because I haven’t touched it for the long time.

• Part 1 - Basic Implementation
• Part 2 - Selection Problems
• Part 3 - 3-way Partitioning

Quick Sort - Duplicate Keys Problem

• Quick Sort goes quadratic unless partitioning stops on equal keys!
• ~½N² compares when all keys equal.
• B A A B A B B B C C C
• A A A A A A A A A A A
• Solve by using 3-way partitioning

3-way Partitioning

Partition array into 3 parts so that:

• Entries between lt and gt equal to partition item v
• No larger entries to left of lt
• No smaller entries to right of gt

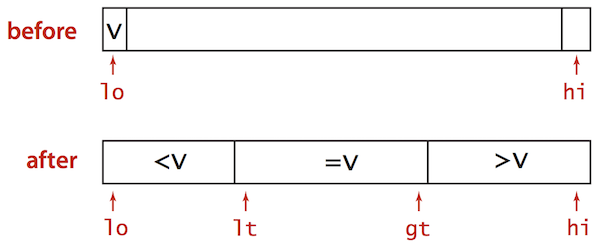
• Let v be partitioning item a[lo]
• Scan i from left to right.
  • (a[i] < v): exchange a[lt] with a[i]; increment both lt and i
  • (a[i] > v): exchange a[gt] with a[i]; decrement gt
  • (a[i] == v): increment i

Java Implementation

private static void sort(Comparable[] a, int lo, int hi) {
    if (hi <= lo) return;
    int lt = lo, gt = hi;
    Comparable v = a[lo];
    int i = lo;
    while (i <= gt)
    {
        int cmp = a[i].compareTo(v);
        if (cmp < 0) exch(a, lt++, i++);
        else if (cmp > 0) exch(a, i, gt--);
        else i++;
    }
    sort(a, lo, lt - 1);
    sort(a, gt + 1, hi);
}

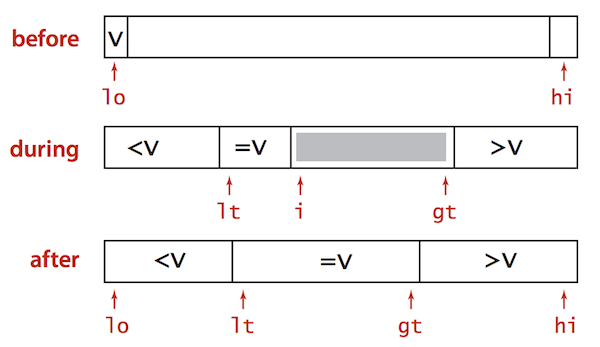
Quick Sort with 3-way partitioning is even shorter (and harder to imagine). I gave one compliment to the brain that could thought of those above solutions.