Nothing special here. It’s just a blog post for summarising my algorithm learning course. Although this was already taught in the University, I didn’t even know that it can be used for Selection Problem

• Part 1 - Basic Implementation
• Part 2 - Selection Problems
• Part 3 - 3-way Partitioning

Selection Problem

Given an array of N items, find a k^th smallest item. For example, an array A = [5, 2, 9, 4, 10, 7], the 3rd smallest item is 5, the 2nd smallest item is 4 and the smallest item is 2

The idea

• Based on Quick Sort
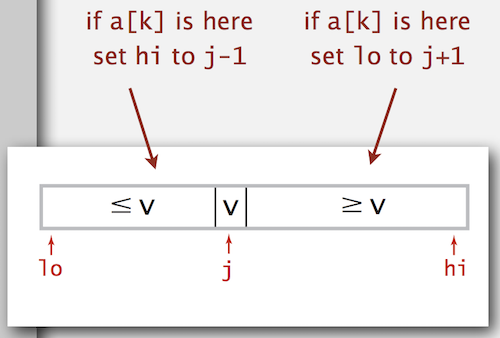
• Partition the array so that
  • Entry a[j] is in place.
  • No larger entry to the left of j
  • No smaller entry to the right of j
• Repeat in one sub-array, depending on j, finished when j equals k

Java Implementation

public static Comparable select(Comparable[] a, int k) {
    StdRandom.shuffle(a);
    int lo = 0, hi = a.length - 1;
    while (hi > lo)
    {
        int j = partition(a, lo, hi);
        if (j < k) lo = j + 1;
        else if (j > k) hi = j - 1;
        else return a[k];
    }
    return a[k];
}

The idea is that, after each partition, the item a[j] will be moved to the right place. So it will become the j^th smallest item. Repeat that process until we can find j = k.

Performance

Quick-select takes linear time on average. Quick-select uses ~½ N² compares in the worst case, but (as with quicksort) the random shuffle provides a probabilistic guarantee.