Nothing special here. It’s just a blog post for summarising my algorithm learning course. Although this was already taught in the University, I remember nothing about it because I haven’t touched it for the long time.
- Part 1 - Basic Implementation
- Part 2 - Selection Problems
- Part 3 - 3-way Partitioning
Quick Sort
The Idea
- Shuffle the array.
- Select one item, can be the first item or last item as the pivot (the partitioned item).
- Partition the array into 2 parts, so that
- The pivot entry is in the right place
- No larger entry to the left of the pivot item
- No smaller entry to the right of pivot item
- Sort each piece recursively.

How to partition the array using the pivot item?
- Select one item as the pivot item
a[lo](the last item in the following gif) - Scan and exchange
- Scan
ifrom left to right so long as (a[i] < a[lo]). - Scan
jfrom right to left so long as (a[j] > a[lo]). - Exchange
a[i]witha[j]. - Repeat until
iandjpointers cross.
- Scan
- Exchange
a[lo]witha[j]
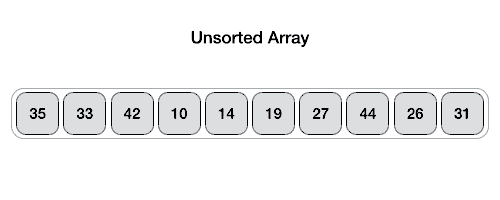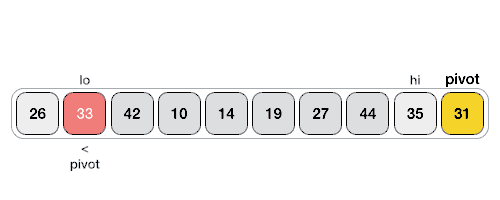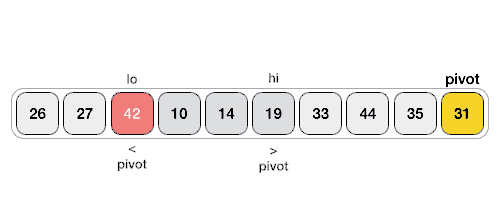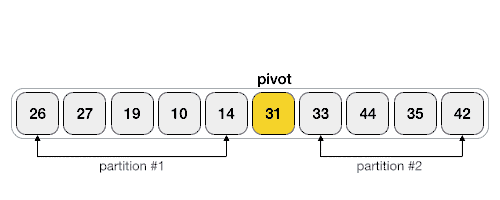
After finish partitioning, all the items on left are smaller than the pivot item, all the items on the right are larger then the pivot, recursively sort each half using quick sort.
Java Implementation
public class Quick {
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo, j = hi + 1;
while (true) {
// find item on left to swap
while (less(a[++i], a[lo]))
if (i == hi) break;
// find item on right to swap
while (less(a[lo], a[--j]))
if (j == lo) break;
// check if pointers cross then swap
if (i >= j) break;
swap(a, i, j);
}
// swap with partitioning item
swap(a, lo, j);
// return index of item now known to be in place
return j;
}
public static void sort(Comparable[] a) {
// shuffle needed for performance guarantee
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
// partition the array into 2 halves
int j = partition(a, lo, hi);
// recursively sort each half
sort(a, lo, j - 1);
sort(a, j + 1, hi);
}
}
Performance Characteristics
- Assume that Laptop executes 108 compares/second.
- Assume that Supercomputer executes 1012 compares/second.
- Insertion sort: N2
- Merge sort N logN
- Quick sort N logN
| insertion | insertion | insertion | merge | merge | merge | quick | quick | quick | |
|---|---|---|---|---|---|---|---|---|---|
| thousand | million | billion | thousand | million | billion | thousand | million | billion | |
| laptop | instant | 2.8h | 317y | instant | 1s | 18m | instant | 0.6s | 12m |
| super | instant | 1s | 1w | instant | instant | instant | instant | instant | instant |
Worst case
- Number of compares is quadratic
- When the array is sorted.
Average case:
- Number of compares is ~ 1.39 N lgN
- 39% more compares than Merge sort
- But faster than Merge sort in practice because of less data movement.
Random shuffle
- Required to prevent the worst case.
- Probabilistic guarantee against worst case.
