It’s not just about Sorting!
1. Merge Sort
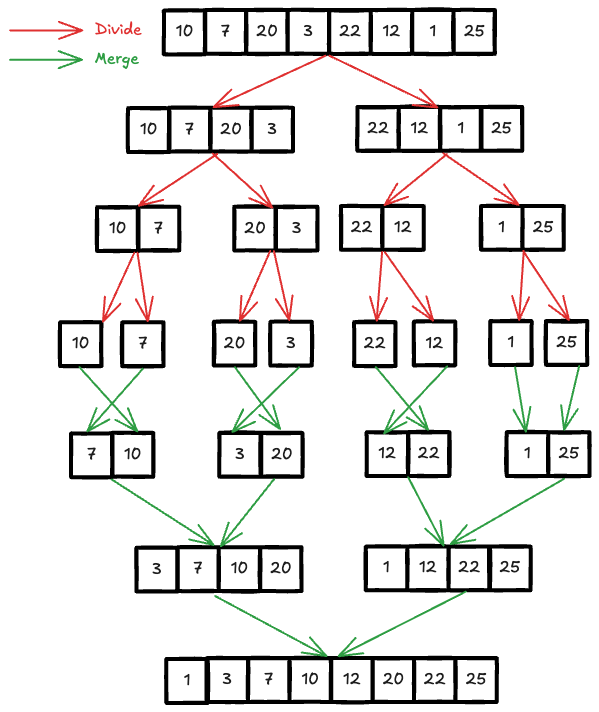
Merge Sort is one of the most commonly taught sorting algorithm (beside Quick Sort) in any Computer Science and Information Technology courses. I will start by briefly reviewing the fundamental knowledge of Merge Sort. The basic idea behind Merge sort is a divide-and-conquer strategy, where you break the array into smaller halves, sort each half and then merge them back together. The recursive process continues until each half contains only 1 item (already sorted).
There are 2 variants of Merge sort implementation, using for and while loop. You can check my
other post about Merge Sort here, which contains
the for version from the algorithm course on Coursera. For the purpose of
interview questions, I’ll demonstrate using the while version in this post.
As mentioned above, there are 2 essential steps in Merge Sort, the Divide step and the Merge step. Let’s begin with the Divide step
// WARNING: This is not working code and not the most efficient way to do
const mergeSort = (arr) => {
// base case
if (arr.length === 1)
return arr;
const mid = Math.floor(arr.length / 2);
const firstHalf = mergeSort(arr.slice(0, mid));
const secondHalf = mergeSort(arr.slice(mid, arr.length));
return merge(firstHalf, secondHalf);
}
and here is how you merge 2 halves (2 sorted arrays)
// WARNING: This is not working code and not the most efficient way to do
const merge = (arr1, arr2) => {
const res = [];
while (arr1.length && arr2.length) {
const item1 = arr1[0];
const item2 = arr2[0];
if (item1 < item2) {
res.push(item1);
arr1.shift();
} else {
res.push(item2);
arr2.shift();
}
}
if (arr1.length) {
res.push(...arr1);
} else {
res.push(...arr2);
}
return res;
}