Optimize a Recursive problem

Ok, you will probably find this problem during your coding interview 😩 Many companies don’t like giving the candidates tricky problems. Instead, they often ask you to write a recursive function to prove that you’re a real engineer, not some random guys applying for the job because it’s well paid 😆 After that, the next question is usually about how to optimize that function with very large datasets and avoid the “Maximum call stack size exceeded” error

Here is how you can prepare yourself for that type of interview question

1. Basic Recursion

Let’s start with this very basic recursion question

Given an array arr with N items, write a recursive function to calculate the sum of all items in the array

If you think about recursion in its simplest form, it’s like a divide and conquer strategy, where you break the problem into smaller ones, solve one of them first and then repeat with the other remaining ones (recursive case) until there is no item left (base case). Now, let’s take a look at the above problem, the solution can be described like this: The sum of an array is the sum of the first element (the head of the list) and all the remaining items (the tail of the array).

If you have worked in any lisp-like language (Emacs Lisp for example 😂), you will immediately see the pattern. They are the car and cdr function in Elisp.

From that, you can easily write a basic recursive function like this (in Javascript)

const sum = (arr) => {
  if (arr.length === 0) {
    return 0;
  }
  const [head, ...tail] = arr;
  return head + sum(tail);
};

An iterative solution

Of course, the easiest way is to convert the above one to a simple for (or while) loop to avoid adding to the call stack.

const sum = (arr) => {
  let sum = 0;
  for (let i=0; i<arr.length; i++) {
    sum += arr[i];
  }
  return sum;
};

Simple? Yeah that’s just what you learnt in university, but that will probably help you during the interview.

Tail-call optimization and Trampoline

Another way you can answer the interviewer is to use Tail-call optimization. In some programming languages, if you return the recursive call as the last expression in the function, they can optimize automatically by avoiding creating a new call stack. Using that concept, you can rewrite the above sum function like this

const sum = (arr, acc) => {
  if (arr.length === 0) {
    return acc;
  }
  const [head, ...tail] = arr;
  return sum(tail, head + acc);
};
sum(arr, 0);

Does it look like Array.prototype.reduce() in Javascript?

However, a new problem arises here. The above piece of code is written in Javascript, which doesn’t support tail-call optimization

Actually, it’s partially supported now. However, let’s assume we are working on a non-supported language.

There is another way you can rewrite the above one in a tail-call style without the support from the language. Instead of returning the recursive call, you can return a function calling the recursive function and use a wrapper function (trampoline) to execute and manage the stack.

const sum = (arr, acc) => {
  if (arr.length === 0) {
    return acc;
  }
  const [head, ...tail] = arr;
  return () => sum(tail, head + acc); // the difference is here
};

const sumTrampoline = (arr) => {
  let result = sum(arr, 0);
  while (typeof result === 'function') {
    result = result();
  }
  return result;
};

sumTrampoline(arr);

2. Dynamic Programming

Now, let’s come to a more complicated problem

You are climbing a staircase. It takes n steps to reach the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

This is the most common DP problem that you will see every time you enter a coding interview (beside the Fibonacci and House Robber question). The most straight forward solution is to write a recursive function to count the ways to step through 1 or 2 steps.

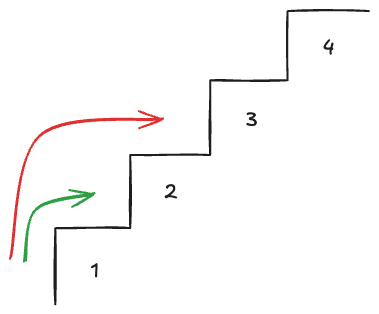
Climb 1

For the above example, the solution can be explained like this

  • Start with count(4)
  • We can climb 1 or 2 steps each time, that means the total ways is the sum of climbing 1 or 2 steps, or count(4) = count(4-2) + count(4-1) = count(2) + count(3)
  • Repeat the same problem with the smaller numbers until there is no more step to climb

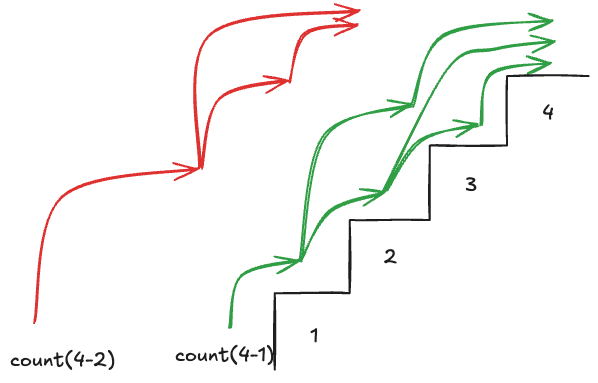
Climb 1

From the above explanation, it’s not hard to come up with the simplest recursive implementation

const count = (n) => {
  // base case: only 1 way to climb if 0 or 1 step
  if (n === 0 || n === 1)
    return 1;

  return count(n - 1) + count(n - 2);
};

const n = 4;
console.log(count(n)); // print 5

Memoization

Let’s take a look at the above solution again, you may notice that both these recursive calls count(2) and count(3) contain an overlapping problem (the blue one in the below picture) because count(3) can be interpreted as count(1) + count(2).

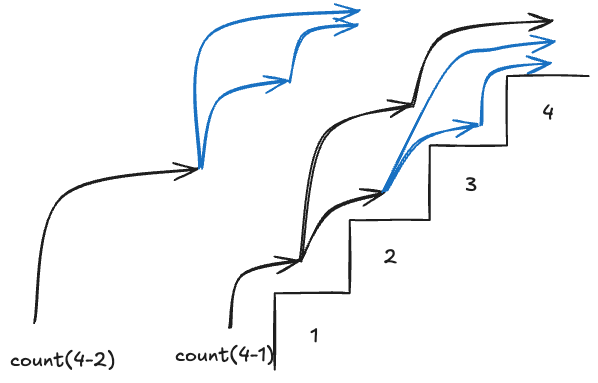
Climb 3

With that in mind, we can store the overlapping calculation into an array and pass that array into each recursive call.

const count = (n, res) => {
  // same base case
  if (n === 0 || n === 1)
    return 1;

  // check if this problem has already been calculated
  if (res[n] !== undefined)
    return res[n];

  res[n] = count(n - 1, res) + count(n - 2, res);
  return res[n];
};

const n = 4;
const res = Array(n + 1);
console.log(count(n, res));

Tabulation

In the above memoization solution, after executing the count function, the res array will be built like this

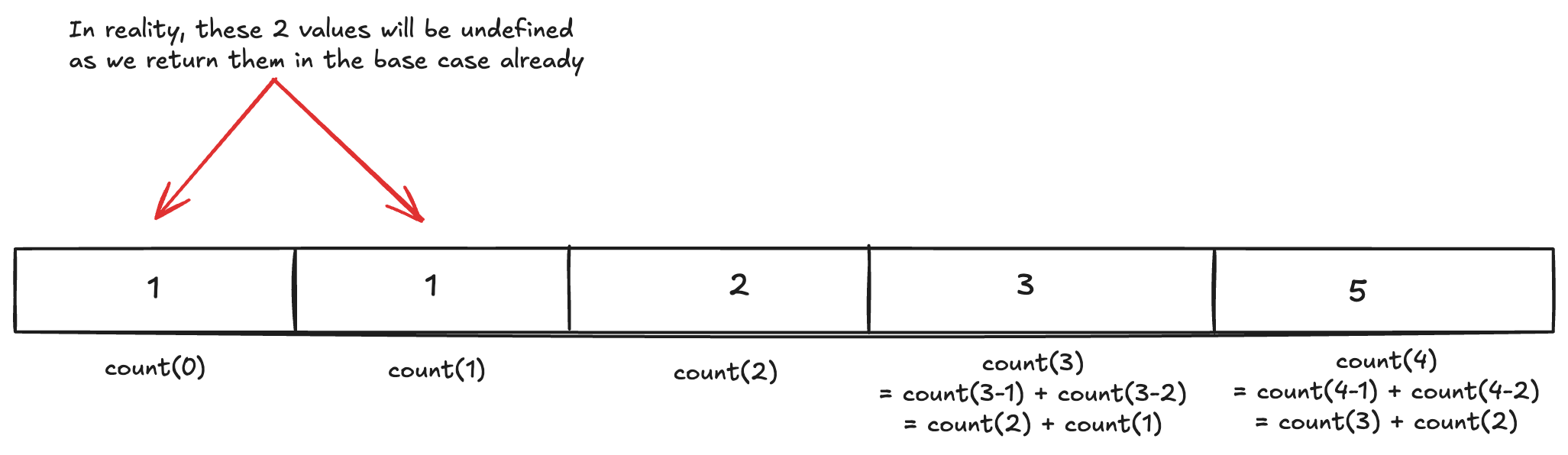
Climb 4

The pattern here is similar to Fibonacci problem, where the value of each item in the array is the value of the previous 2 items. We can then build a solution to traverse and build the array from the beginning

const count = (n) => {
  const res = Array(n + 1);

  // base case
  res[0] = 1;
  res[1] = 1;

  for (let i=2; i<=n; i++) {
    res[i] = res[i-1] + res[i-2];
  }
  return res[n];
}

const n = 4;
console.log(count(n));

You can also optimize it even more using only 2 variables to store i-1 and i-2 values.

3. Depth First Search and Breadth First Search

Another type of recursion question that the interviewer usually ask is the question related to tree data structure, for example this one

Given a starting directory, build a JSON model representing the structure of the directory and all its nested items. Your function should output a json structure like this

{
  "name": "root",
  "contents": [
    "file.txt",
    {
      "name": "root/folder1",
      "contents": [
        "weavels.pdf"
      ]
    },
    {
      "name": "root/an_empty_folder",
      "contents": []
    },
    "test.txt"
  ]
}
  • Each file is represented as a string
  • Each folder is represented as an object with a contents array for all its child { "name": "xxx", "contents": []}

I was quite surprised that many engineers couldn’t solve this problem using the simplest recursive implementation 🫠

At the very basic level, a software engineer should be able to write a simple recursive function like this to traverse the directory tree starting from the root node

const getContents = (path) => {
  // implement this
  return ['child1.js', 'child2.txt', 'childFolder1'];
}

const isFolder = (path) => {
  // implement this
  return true;
}

const buildNode = (parent) => {
  const children = getContents(parent.name);
  
  for (let i = 0; i < children.length; i++) {
    const name = children[i];
    const childNode = isFolder(name) ?
      buildNode({name, contents: []}) : name;
    parent.contents.push(childNode);
  }
  
  return parent;
}

const res = buildNode({name: entryPoint, contents: []});

After you have finished writing that, the interviewer will definitely ask a follow up question about your optimization when the input folder is a very big one with a lot of nested levels. There are many ways to solve this, but the most common way is to convert this to a Breadth First Search solution.

As long as you can mention that keyword, you are 50% to the success 😆

The idea behind BFS is to visit all nodes in the current level first (closest nodes first) before visiting the next level (further ones later), in constrast to DFS, that is to traverse all the nested child of the current node before visiting the next one. BFS can help you avoid the “Maximum call stack exceeded” error in DFS for very large trees. The implementation relies on a queue and sometimes an extra array to store the visited items.

Here is the quick and dirty BFS solution

const buildTree = (entryPoint) => {
  const root = {name: entryPoint, contents: []};
  const q = [root]; // use array for bfs queue
  
  while (q.length) {
    const current = q.pop();
    const children = getContents(current.name);
    children.forEach(child => {
      if (isFolder(child)) {
        const childNode = {name: child, contents: []};
        q.push(childNode);
        current.contents.push(childNode);
      } else {
        current.contents.push(child);
      }
    });
  }
  
  return root;
}

You can also use BFS for Binary tree, 2D maze and Unweighted graph problems

Time to practice

What I presented in this post so far are just the suggestions to the common recursive problems. They are not everything but can cover most of the interview questions related to recursion. I’ve been through several similar interviews and even the advanced problems given to Senior role are based on those 3 categories with a lot more edge cases to handle (FAANG and Big Tech interview could be different and harder).

You should also practice to get yourself familiar with those types of question before any interview. Here are some challenges that you could take