Nothing special here. It’s just a blog post for summarising my algorithm learning course. Probably this was taught in the University but I don’t remember anything, I have no idea about its definition and applications until I take this course.

Heap-ordered Binary Tree

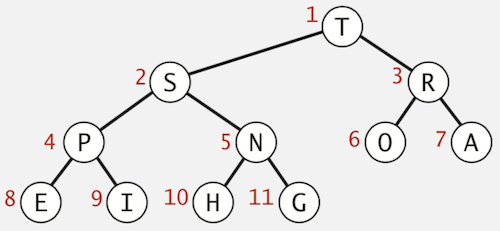
• Each node represents a key
• Parent’s key is not smaller than children’s keys

Array Representation

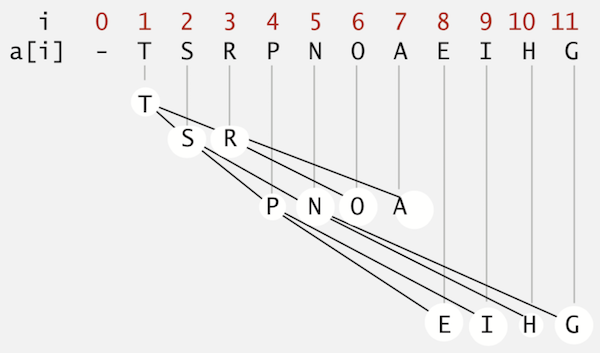
• Indices start at 1.
• Take nodes in level order.
• No explicit links needed!
• Largest key is a[1], which is root of binary tree
• Can use array indices to move through tree
  • Parent of node at k is at k/2
  • Children of node at k are at 2k and 2k+1

Promotion in a heap

• Scenario: Child’s key becomes larger key than its parent’s key.
• To eliminate the violation:
  • Exchange key in child with key in parent.
  • Repeat until heap order restored.
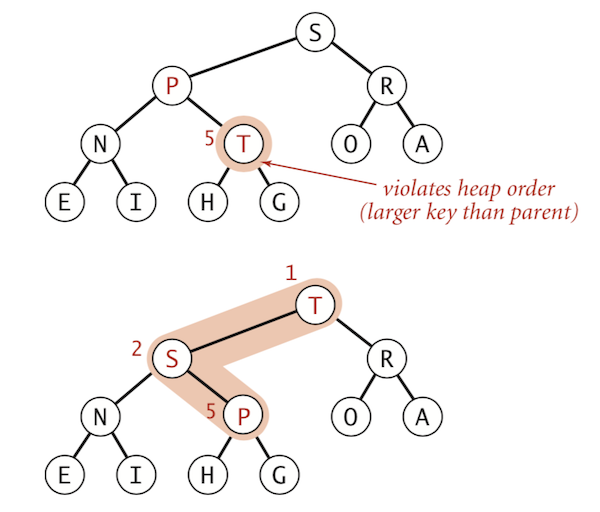
• In the below image, the 5th item T is not in the correct order
  • T is larger than P (its parent), exchange
  • T is still larger than S (its parent), exchange
  • Finally, T is in the correct order

private void swim(int k) {
    while (k > 1 && less(k/2, k)) {
        exch(k, k/2);
        k = k/2;
    }
}

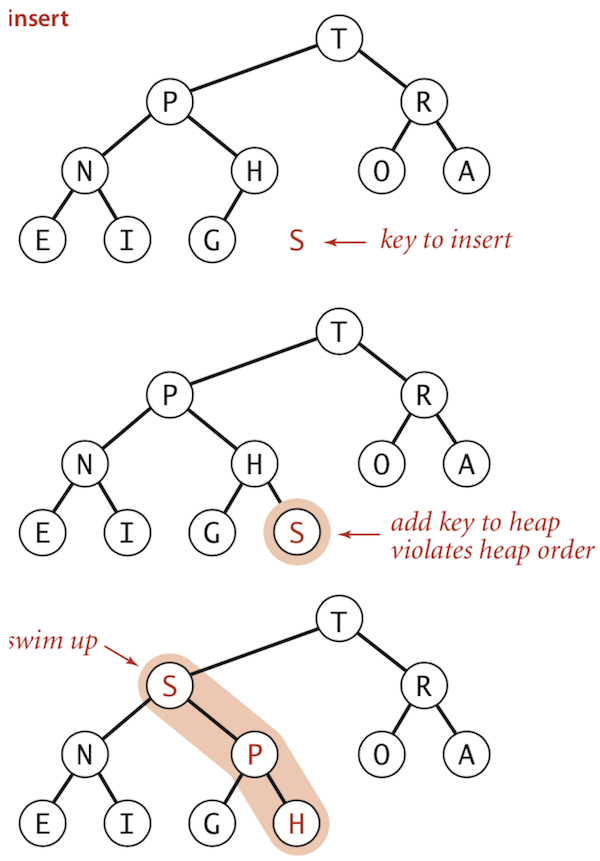
Insertion in a heap

• Add node at end, then swim it up.
• Cost: At most 1 + lgN compares.

public void insert(Key x) {
    pq[++N] = x;
    swim(N);
}

Demotion in a heap

• Scenario: Parent’s key becomes smaller than one (or both) of its children’s.
• To eliminate the violation:
  • Exchange key in parent with key in larger child.
  • Repeat until heap order restored.
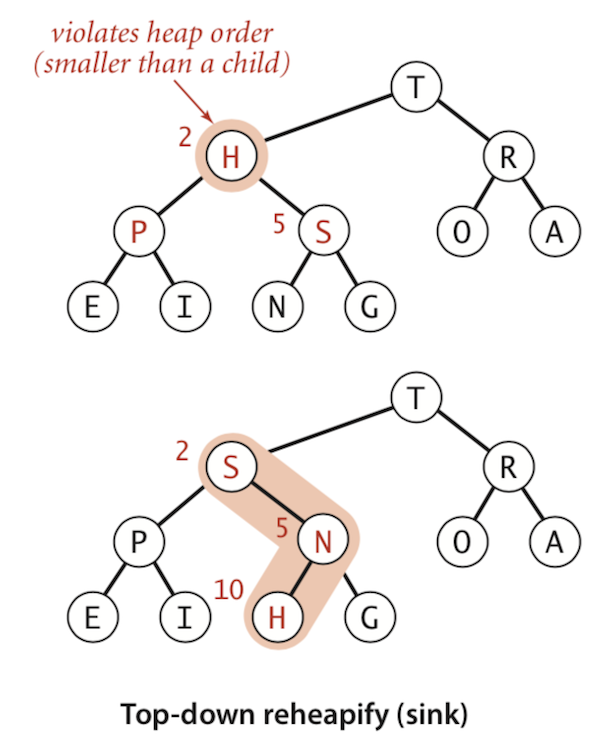
• In the below image, the 2nd item H is not in the right order
  • H is smaller than its children, exchange with the larger child S
  • H is still smaller than its children, exchange with the larger child N
  • Finally, H is in the correct order

private void sink(int k) {
    while (2*k <= N) {
        int j = 2*k;
        // children of node at k are 2k and 2k+1, decide which one is larger
        if (j < N && less(j, j+1)) j++;
        // when the item is in the right order, stop
        if (!less(k, j)) break;
        // otherwise, exchange
        exch(k, j);
        k = j;
    }
}

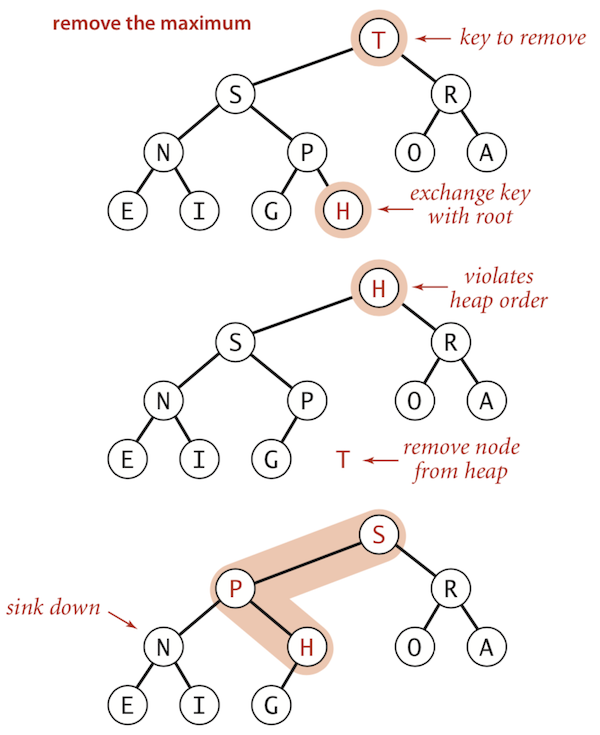
Delete the Maximum in a heap

• Exchange root with node at end, then sink it down.
• Cost: At most 2 lgN compares.

public Key delMax() {
    Key max = pq[1];
    exch(1, N--);
    sink(1);
    // prevent lotering
    pq[N+1] = null;
    return max;
}

To be continued

Part 2 Binary Heap and Heapsort Summary - Part 2 - Heapsort