Nothing special here. It’s just a blog post for summarising my algorithm learning course. Probably this was taught in the University but I don’t remember anything, I have no idea about its definition and applications until I take this course. Part 1 here Binary Heap & Heapsort Summary - Part 1 - Binary Heap
The Idea
- Start with array of keys in arbitrary order
- Create max-heap with all N keys.
- Repeatedly remove the maximum key (in place) to create a sorted array.
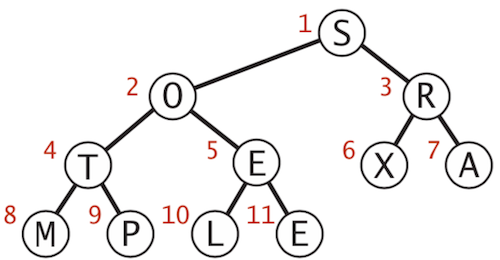
First step: Heap construction
Build heap using bottom-up method. Start with the lowest nodes and go up each level, use sink
operation to correct the heap.
- Starting point (arbitrary order)
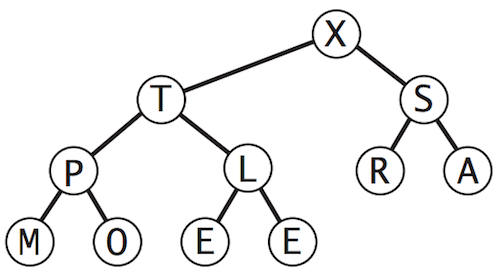
- All the nodes in the lowest level are 1-node binary heap. In this case
E,L,PandMare already in sorted order (1-node binary heaps). - Start with the nodes in the upper level,
X,A,EandTin this caseXandAare already 1-node binary heaps- Apply
sink(5)operation onEto make it a sorted binary heap
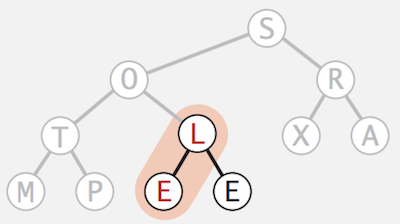
- Apply
sink(4)operation onT, nothing to do here because it’s already a sorted binary heap
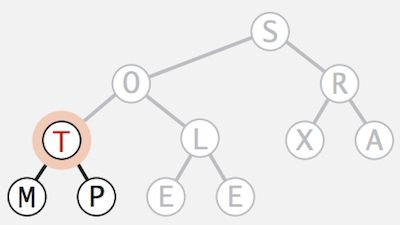
- Continue with the nodes in higher level,
XandOin this case- Apply
sink(3)operation onRto make it a sorted binary heap
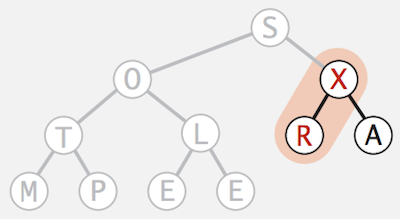
- Apply
sink(2)operation onOto make it a sorted binary heap
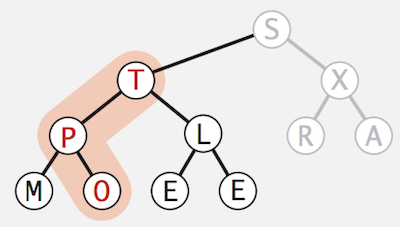
- Apply
- Continue with the node in the highest level,
Sin this case- Apply
sink(1)operation onSto make it a sorted binary heap
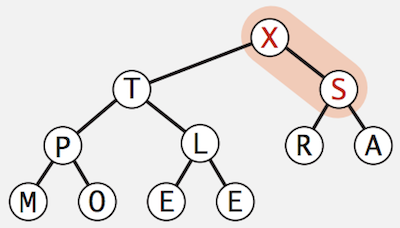
- Apply
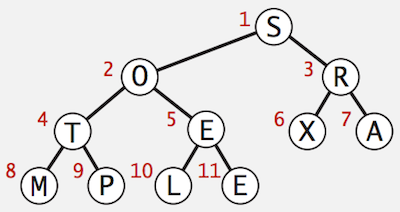
- We finally transform an arbitrary array into a heap-ordered array
for (int k = N/2; k >= 1; k--)
sink(a, k, N);
Second step: Sortdown
In order to transform a heap-ordered array into a sorted array, we will repeatedly remove the largest item in the heap, one at a time. Refer to part 1 for the idea on how to remove the maximum item in a heap. The only difference is that after exchanging the max with the last item, we will keep it in the array instead of completely removing it out.
- Starting point (a heap-ordered array)
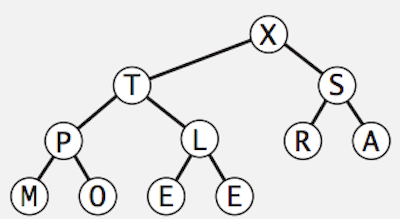
- Repeatedly remove the largest item, once at a time, keep it at the end of the array

while (N > 1) {
swap(a, 1, N--);
sink(a, 1, N);
}
Java Implementation
public class Heap {
public static void sort(Comparable[] a) {
int N = a.length;
// build the heap
for (int k = N/2; k >= 1; k--)
sink(a, k, N);
// convert heap to sorted array
while (N > 1)
{
exch(a, 1, N);
sink(a, 1, --N);
}
}
private static void sink(Comparable[] a, int k, int N) {
// implemented in part 1
}
private static boolean less(Comparable[] a, int i, int j) { /* compare */ }
private static void swap(Comparable[] a, int i, int j) { /* swap */ }
}
Heapsort Characteristics
Heapsortis an In-place sorting algorithm withN logNworst-case- Compare to the other sorting algorithm
Mergesort: not in-place, linear extra space required.Quicksort: in-place, but quadratic time in worst case.
Heapsortis optimal for both time and space, but:- Inner loop longer than
Quicksort’s - Makes poor use of cache memory
- Inner loop longer than
