just a blog post for summarising my algorithm course
The Problem
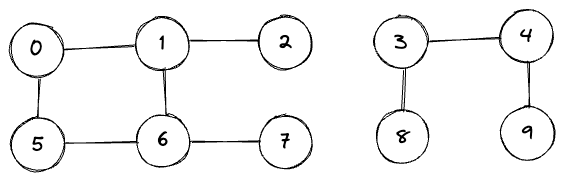
Given a data structure organised as a set of N objects, is there a path connecting 2 objects?
// union: connect 2 objects
// connected: whether 2 objects are connected?
union(4, 3);
union(3, 8);
union(6, 5);
union(9, 4);
union(2, 1);
connected(0, 7) return false;
connected(8, 9) return true;
union(5, 0);
union(7, 2);
union(6, 1);
union(1, 0);
connected(0, 7) return true;
Can only answer the question with Yes or No. The Dynamic Connectivity implementation cannot
answer the exact path between 2 objects. It can only answer whether there are any paths connecting 2
objects.
Interface
The Union Find data type contains these 2 main methods
class UnionFind {
union(p: number, q: number): void {...}
connected(p: number, q: number): boolean {...}
}
Quick Find
The Quick Find idea is to assign all the items in 1 connected component with 1 same id. p and
q are connected if they have the same id. Every time we do the union command, we update those 2
items with the same id (and also all other items in the connected component).
The set is organised as an array, where the values are the id of that connected component. At first,
all the items have the id the same with its index (connected to itself). After each call to union,
we update the id of those 2 items to one of them
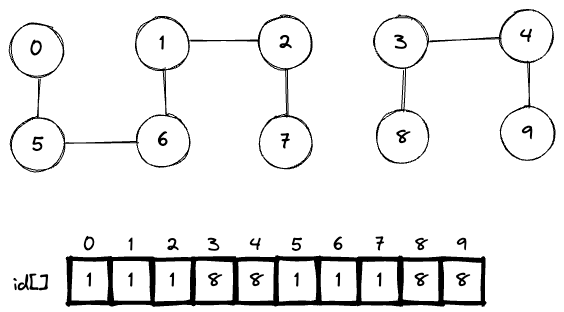
To check whether the 2 items are connected, simply check whether they have the same id or not. For example
connected(6, 7)=>truebecause 6 and 7 both have id1connected(0, 9)=>falsebecause 0 has the id1and 9 has the id8
Here is the complexity analysis
| Method | Complexity | |
|---|---|---|
isConnected(p, q) |
O(1) | Only 1 call to check the id of the item |
union(p, q) |
O(n^2) | Have to update id of both items and all other items having the same id |
The implementation is so easy, won’t post here
Quick Union
Use Quick Union to solve the above Union problem of Quick Find
The underlying data structure for Quick Union is similar to Quick Find. We need an array for all
the items. The values are still the id, but it’s the id of the parent item. The connected component
is organised using a tree structure like this

After doing the union

In short
isConnected(p, q)check whether the 2 items have the same rootunion(p, q)set the id of p’s root to the id of q’s root
Here is the sample implementation of Quick Union in TS
class UnionFind {
_id: number[];
constructor(n: number) {
// set id of each object to itself
this._id = [...Array(n).keys()];
}
root(i: number): number {
// chase parent pointers until reach root
while (i != this._id[i]) i = this._id[i];
return i;
}
union(p: number, q: number): void {
// change root of p to point to root of q
const i = this.root(p);
const j = this.root(q);
this._id[i] = j;
}
connected(p: number, q: number): boolean {
// check if p and q have same root
return this.root(p) === this.root(q);
}
}
Complexity analysis
| Method | Complexity | |
|---|---|---|
isConnected(p, q) |
O(N) | Worst case, have to traverse through all items |
union(p, q) |
O(n) | Only need to update 1 id but including the cost of finding roots |
=> Quick Union is faster than Quick Find when performing isConnected command but still too slow
for large data set.
Weighted Quick Union
- Use
Quick Unionbut avoid tall tree, to avoid traversing through very long path - Use an extra array to track the size of each tree (stored in the root node)
- Link the smaller tree to the root of the larger tree
- The size of the new tree is the total size of both tree
| Method | Complexity | |
|---|---|---|
isConnected(p, q) |
O(lgN) |
Depth of any node x is at most lgN |
union(p, q) |
O(lgN) |
Quick Union with Path Compression
- Use
Quick Unionbut try to flatten the tree - Every time we compute the root of one item (by traversing through the path to the root), set that item to point directly to the root.
- Next time when we call the function to find the root of that same item, we don’t have to traverse through the full path again
For example, instead of linking 9 to 6

we can simply link it directly to the root of 6 (which is 0)

For path compression, if the root is called many times enough, the complexity will become O(1)
when the tree become flatten.
