Nothing special here. It’s just a blog post for summarising my algorithm learning course. Although this was already taught in the University, it’s still god to summarize here

1. Symbol Tables

Key-value pair abstraction.

• Insert a value with specified key.
• Given a key, search for the corresponding value.

Example

Symbol Table APIs

Symbol Tables act as an associative array, associate one value with each key.

public class ST<Key, Value> {
    void put(Key key, Value, val);
    Value get(Key key);
    void delete(Key key);
    boolean contains(Key key);
    boolean isEmpty();
    int size();
    Iterable<Key> keys();
}

2. Ordered Symbol Tables

If we order the keys in Symbol table, we can support a much wider number of operations, for example min, max operations and especially range operations.

| operations                    | keys     | values  |
|-------------------------------|----------|---------|
| min() ======================> | 09:00:00 | Chicago |
|                               | 09:00:03 | Phoenix |
| get(09:00:13) ==============> | 09:00:13 | Houston |
|                               | 09:00:59 | Chicago |
|                               | 09:01:10 | Houston |
| floor(09:05:00) ============> | 09:03:13 | Chicago |
|                               | 09:10:11 | Seattle |
| select(7) ==================> | 09:10:25 | Seattle |
|                               | 09:14:25 | Phoenix |
| ============================> | 09:19:32 | Chicago |
| ============================> | 09:19:46 | Chicago |
| keys(09:15:00, 09:25:00) ===> | 09:21:05 | Chicago |
| ============================> | 09:22:43 | Seattle |
| ============================> | 09:22:54 | Seattle |
|                               | 09:25:52 | Chicago |
| ceiling(09:30:00) ==========> | 09:35:21 | Chicago |
|                               | 09:36:14 | Seattle |
| max() ======================> | 09:37:44 | Phoenix |
| size(09:15:00, 09:25:00) = 5  |          |         |
| rank(09:10:25) = 7            |          |         |

Ordered Symbol Table APIs

public class ST<Key extends Comparable<Key>, Value> {
    void put(Key key, Value val);
    Value get(Key key);
    void delete(Key key);
    boolean contains(Key key);
    boolean isEmpty();
    Key min();
    Key max();
    Key floor(Key key);
    Key ceiling(Key key);
    int rank(Key key); // number of keys less than key
    Key select(int k); // select key of rank k
    void deleteMin();
    void deleteMax();
    // range operations
    int size(); // size of the whole tree
    int size(Key lo, Key hi); // size of range
    Iterable<Key> keys(); // iterate through all keys
    Iterable<Key> keys(Key lo, Key hi); // iterate though keys in range
}

3. Binary Search Tress

Binary Search Tree is a binary tree in symmetric order. Each node has a key, and every node’s key is

• Larger than all keys in its left subtree.
• Smaller than all keys in its right subtree

In the tree above, every key is larger than all keys in its left subtree and smaller than all keys in its right subtree (for example A < C < E < H < M < R < S < X).

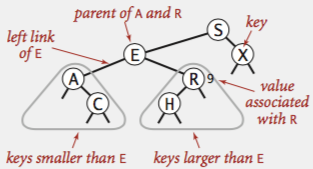
Using BST, we can implement all the operations of Ordered Symbol Tables quite efficiently, as long as keys are inserted in random order.

Node

A Binary Search Tree is a reference to the root Node

class Node {
   private Key key;
   private Value val;
   private Node left, right;
   public Node(Key key, Value val) {
      this.key = key;
      this.val = val;
   }
}

Get method

Return value corresponding to given key, or null if no such key. Traverse from the root node, if less, go left, if greater, go right, if equal, search hit.

public Value get(Key key) {
   Node x = root;
   while (x != null) {
      int cmp = key.compareTo(x.key);
      if      (cmp  < 0) x = x.left;
      else if (cmp  > 0) x = x.right;
      else if (cmp == 0) return x.val;
   }
   return null;
}

Insert method

Search for key, then two cases:

• Key in tree ⇒ reset value.
• Key not in tree ⇒ add new node.

private Node put(Node x, Key key, Value val) {
    if (x == null) return new Node(key, val);

    int cmp = key.compareTo(x.key);
    if  (cmp  < 0)
        x.left  = put(x.left,  key, val);
    else if (cmp  > 0)
        x.right = put(x.right, key, val);
    else if (cmp == 0)
        x.val = val;
    return x;
}

Floor/Ceiling method

Floor: Largest key ≤ a given key

• Case 1: k equals the key at root
  • The floor of k is k
• Case 2: k is less than the key at root
  • The floor of k is in the left subtree.
• Case 3: k is greater than the key at root
  • The floor of k is in the right subtree if there is any key ≤ k in right subtree
  • Otherwise it is the key in the root.

private Node floor(Node x, Key key) {
   if (x == null) return null;
   int cmp = key.compareTo(x.key);

   if (cmp == 0)
       return x;
   if (cmp < 0)
       return floor(x.left, key);

   Node t = floor(x.right, key);
   if (t != null)
       return t;
   else
       return x;
}

Ceiling: the reverse way

Subtree counts

In each node, we store the number of nodes in the subtree rooted at that node; To implement size(), return the count at the root.

Rank. How many keys < k ?

Store the size of each subtree in its root node. rank then walks down the tree, adding up the sizes of the left subtrees it skips over:

For example, to compute rank("R") (the number of keys smaller than R):

• R < S, go left into E.
• R > E, so skip E and its whole left subtree: 1 + size(A subtree) = 1 + 2 = 3, then continue into E’s right child R.
• R == R, add size(left subtree of R) = 2.
• Total: 3 + 2 = 5, matching the keys A, C, E, H, M.

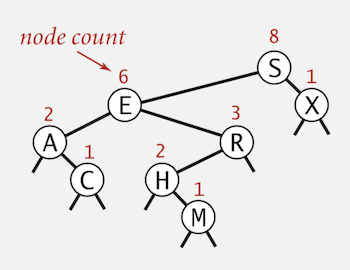
public int rank(Key key) {
    return rank(key, root);
}

private int rank(Key key, Node x) {
   if (x == null) return 0;

   int cmp = key.compareTo(x.key);
   if      (cmp  < 0)
       return rank(key, x.left);
   else if (cmp  > 0)
       return 1 + size(x.left) + rank(key, x.right);
   else if (cmp == 0)
       return size(x.left);
}

In-Order Traversal

• Traverse left subtree.
• Enqueue key.
• Traverse right subtree.

public Iterable<Key> keys() {
    Queue<Key> q = new Queue<Key>();
    inorder(root, q);
    return q;
}

private void inorder(Node x, Queue<Key> q) {
   if (x == null) return;

   inorder(x.left, q);
   q.enqueue(x.key);
   inorder(x.right, q);
}

In-Order traversal of a BST yields keys in ascending order

Lazy Deletion

To remove a node with a given key:

• Set its value to null.
• Leave key in tree to guide search (but don’t consider it equal in search)

Here the key E is tombstoned: its value is set to null, but the key stays so that searches can still be routed correctly to its children A and R:

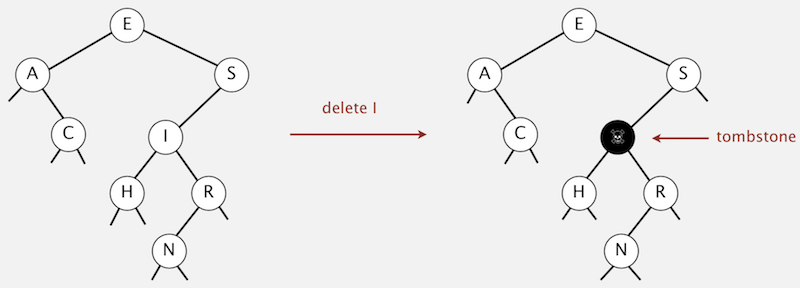
Drawback: Tombstone (memory) overload

Delete the minimum

To delete the minimum key:

• Go left until finding a node with a null left link.
• Replace that node by its right link.
• Update subtree counts.

public void deleteMin() {
    root = deleteMin(root);
}

private Node deleteMin(Node x) {
   if (x.left == null) return x.right;

   x.left = deleteMin(x.left);
   x.count = 1 + size(x.left) + size(x.right);
   return x;
}

Delete a specific key using Hibbard deletion

To delete a node with key k, search for the node t containing key k, then handle three cases.

Case 0 - t has 0 children: delete t by setting its parent link to null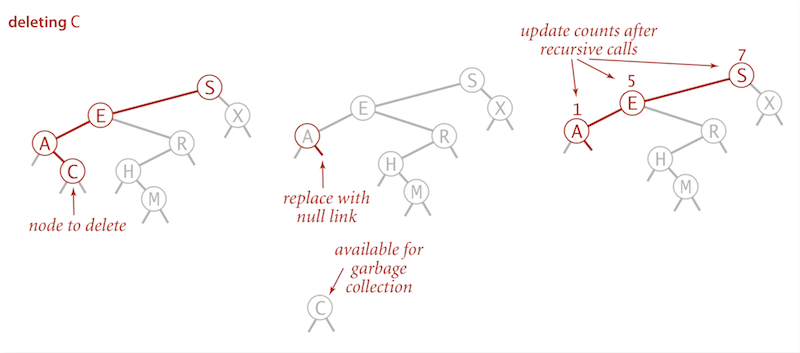. Here we remove the leaf A:

Before

After

Case 1 - t has 1 child: delete t by replacing its parent link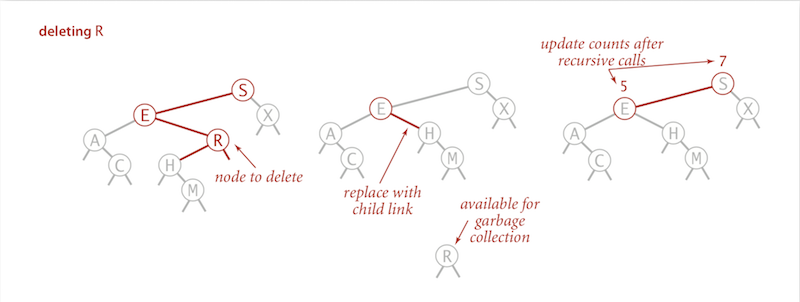 with t’s only child. Here we remove E, whose only child is R:

Before

After

Case 2 - t has 2 children (Hibbard deletion):

• Find the successor x of t - the minimum of t.right.
• Delete x out of the BST using the deleteMin method, but keep the node x in memory.
• Put x in t’s spot.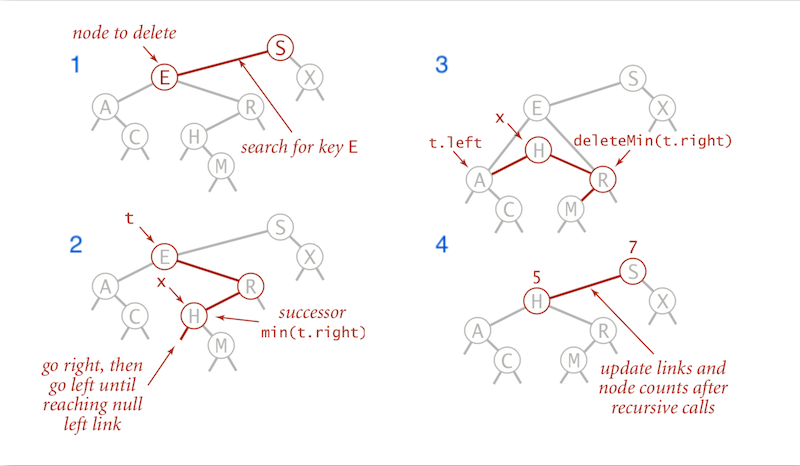

Here we delete E; its successor is H (the minimum of E’s right subtree), which moves up into E’s position:

Before

After

public void delete(Key key) {
    root = delete(root, key);
}

// delete method returns the new tree after deletion
private Node delete(Node x, Key key) {
    if (x == null) return null;

    // search for key by traserving left/right
    int cmp = key.compareTo(x.key);
    if (cmp < 0)
        // set the subtree to the new tree after deletion
        x.left  = delete(x.left,  key);
    else if (cmp > 0)
        // set the subtree to the new tree after deletion
        x.right = delete(x.right, key);

    else {
        // case 0 and case 1, return null or the left/right subtree to
        // update the link in parent node
        if (x.right == null) return x.left;
        if (x.left  == null) return x.right;

        // case 2, replace with successor
        Node t = x;
        x = min(t.right);
        x.right = deleteMin(t.right);
        x.left = t.left;
    }

    // update subtree counts
    x.count = size(x.left) + size(x.right) + 1;
    return x;
}