Nothing special here. It’s just a blog post for summarising my algorithm learning course. Although this was already taught in the University, it’s still good to summarise here

1. Stacks

Last In First Out

Linked-list Implementation

Maintain a pointer to the first item of the linked-list. Add or remove are simply to update that pointer.

class Node {
  item: string;
  next: Node;

  constructor(item: string, next: Node) {
    this.item = item;
    this.next = next;
  }
}

class Stack {
  first: Node;

  push = (item: string): void => {
    const oldFirst = this.first;
    this.first = new Node(item, oldFirst);
  }

  pop = (): string => {
    const item = this.first.item;
    this.first = this.first.next;
    return item;
  }
}

Array Implementation

• Use array s[] to store N items on stack
• push(): add new item at s[N]
• pop(): remove item from s[N-1]

Resizing-array Implementation

• Start with array size 1
• push(): double size of array when full and copy all items
• pop(): halve size of array when array is one-quarter full

Amortized time (average time): constant because we access the item directly in the array, only slow when double size of array, but we won’t do it very frequently. It happen lgN times.

One interesting thing I found is that Golang slices is implemented this way (from what I read from the Go book), but yeah, I have to check again to make sure because I have never worked with Go yet.

Comparison

Linked-list implementation

• Every operation takes constant time in the worst case
• Uses extra time and space to deal with the links.

Resizing-array implementation

• Every operation takes constant amortized time
• Less wasted space

Actually, Resizing-array implementation will be helpful a lot in implementing a randomized queue. See below

2. Queues

First In First Out

Linked-list Implementation

Maintain 2 pointers to the first and last items of the linked-list. Enqueue or dequeue are simply to update those pointers

class Node {
  item: string;
  next: Node;
}

class Queue {
  first: Node;
  last: Node;

  enqueue = (item: string): void => {
    const oldLast = this.last;
    this.last = new Node();
    this.last.item = item;
    this.last.next = null;
    if (isEmpty()) this.first = this.last;
    else oldLast.next = this.last;
  }

  dequeue = (): string => {
    const item = this.first.item;
    this.first = this.first.next;
    if (isEmpty()) last = null;
    return item;
  }
}

Array Implementation

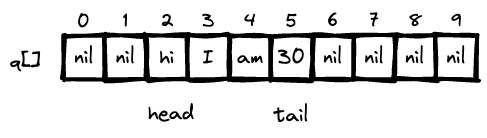
• Use array q[] to store items in queue
• Use 2 pointers to store the index of head and tail
• enqueue(): add new item at q[tail]
• dequeue(): remove item from q[head]
• The index can goes out of the array range. Use modulo to get the correct index.
• Apply resizing array like Stack’s Array Implementation

3. Double-Ended Queues - Deques

A double-ended queue or deque (pronounced “deck”) is a generalization of a stack and a queue that supports adding and removing items from either the front or the back of the data structure.

By using a doubly linked-list, we can achieve constant worst-case time for all the Deque operation (including constructor). The sample working implementation can be found here.

4. Randomized Queues

A randomized queue is similar to a stack or queue, except that the item removed is chosen uniformly at random from items in the data structure.

An Resizing-Array implementation supports each randomized queue operation a constant amortized processing time. The implementation is the same as the Queue’s Resizing Array Implementation. To enqueue, we still add new item at q[tail]. The only difference is the dequeue method. To dequeue, we will pick a random item in the array, move the last item into that position and return that random item. The sample working implementation can be found here.

5. Stack with Max

Stack with Max is another data structure that efficiently supports the stack operations (push and pop) and also a return-the-maximum operation. To implement that, simply use 2 stacks, one to store all the items just like the Stack implementation above, the other one to store the maximum values.

class Node {
  item: number;
  next: Node;
}

class MaxStack {
  // ...similar to stack implementation

  // for maxStack
  max: Node;

  getMax = (): number => this.max.item;

  push = (item: number): void => {
    // ...similar to stack implementation

    // store max value
    if (item > this.getMax()) {
      const oldMax = this.max;
      this.max = new Node();
      this.max.next = oldMax;
    }
  }

  pop = (): number => {
    // ...similar to stack implementation

    if (tmp === this.getMax()) {
      this.max = this.max.next;
    }
    return tmp;
  }
}